20210710-CTFSHOW CJB-CryptoSecPartWriteUp

Posted on Edited on In , Views: Symbols count in article: 18k Reading time ≈ 17 mins.

 

Cop! Run!!

la佬出的题目

题目描述 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
from Crypto.Util.number import *
from flag import flag

n = 1 << 8
p = getPrime(n)
print(p)

P.<t> = PolynomialRing(Zmod(p))
f = t * t + randrange(p)
print(f)

x = [randrange(p)]
x += [f(x[0])]
print([x_ >> (n - ceil(5 * n / 7)) for x_ in x])

flag = bytes_to_long(flag)
y = f(x[-1])
for i in range(7):
    y = f(y)
    flag ^^= int(y)
print(flag)

'''
92946459607669937513774102250057295249718593723232674702212854287358873135783
t^2 + 43844336985235863734419631630425915388298791521868754583032904718644333115590
[3248642833056635029095920782095626337949113592116495266, 4883935221919623989344404485025479346028101682781790392]
193207529097125793778662519051231322609402866155819915933598367395102313904490702547833
'''

hint

1
Brad Pitt & Angelina Jolie love each other hard in some movie.

解题思路

题目中出现Cop，猜测是CopperSmith；从hint中获悉，一部零五年的电影《Mr Smith & Mrs Smith》，是CopperSmith没跑了

先看代码，代码很简短，显然只要求出 x 的前两项，所有的问题就迎刃而解，或者说，只要知道 x[1] ，就可以求出 y ，然后依据异或的性质，加密即解密

而我们已知的是 x 右移73位的数据，显然是要求低位。自然而然可以想到方程的思想，设置几个变量，然后根据等式解方程。因为前面接触过 CopperSmith 在 RSA 中的应用，sage 里的 smal_roots 就是基于 CopperSmith 实现的

下面简单介绍一下 CopperSmith ，摘自CTF Wiki

CopperSmith基本原理

Coppersmith 相关攻击与 Don Coppersmith 紧密相关，他提出了一种针对于模多项式（单变量，二元变量，甚至多元变量）找所有小整数根的多项式时间的方法。

这里我们以单变量为主进行介绍，假设

  • 模数为 N ，N 具有一个因子$b≥N^β,0<β≤1$
  • 多项式 F 的次数为$δ$

那么该方法可以在$O(cδ^5log^9(N))$的复杂度内找到该多项式所有的根$x_0$，这里我们要求 $|x_0|<cN^\frac{β^2}{δ}$。

在这个问题中，我们的目标是找到在模 N 意义下多项式所有的根，这一问题被认为是复杂的。Coppersmith method 主要是通过 Lenstra–Lenstra–Lovász lattice basis reduction algorithm（LLL）方法找到

  • 与该多项式具有相同根 $x_0$
  • 更小系数
  • 定义域为整数域

的多项式 g，由于在整数域上找多项式的根是简单的（Berlekamp–Zassenhaus），从而我们就得到了原多项式在模意义下的整数根。

那么问题的关键就是如何将 f 转换到 g 呢？Howgrave-Graham 给出了一种思路

image-20180717210921382

也就是说我们需要找到一个具有 “更小系数” 的多项式 g，也就是下面的转换方式

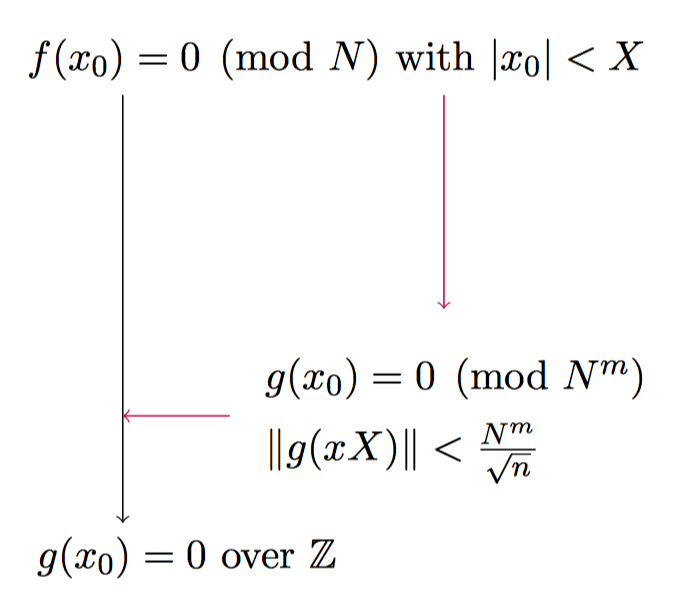
image-20180717211351350

在 LLL 算法中，有两点是非常有用的

  • 只对原来的基向量进行整数线性变换，这可以使得我们在得到 g 时，仍然以原来的 $x_0$ 为根。
  • 生成的新的基向量的模长是有界的，这可以使得我们利用 Howgrave-Graham 定理。

在这样的基础之上，我们再构造出多项式族 g 就可以了。

关于更加细节的内容，请自行搜索。同时这部分内容也会不断更新。

需要注意的是，由于 Coppersmith 根的约束，在 RSA 中的应用时，往往只适用于 e 较小的情况。

总结，CopperSmith 可以用来一元甚至多元的多项式

回到题目，初步尝试，在尚师傅的指导下，我写出来了第一个多项式，设 $x_{0}$ 的低73位为 k
$$
f(x_{0}<<73+k)>>73=x_{1}\notag
$$
是关于 k 的一元多项式，然后我们尝试能不能解

la佬的博客上有解一元和多元的脚本

1
2
3
4
5
6
7
8
9
10
11
12
#Sage
#单元
PR.<x> = PolynomialRing(Zmod(n))
f = (a + x)^e - c
root = f.small_roots(X=2^256, beta=1)[0]  # find root < 2^256 with factor = n

#多元
load('coppersmith.sage')
P.<x, y> = PolynomialRing(GF(p))
f = 2^170 * a^2 + 2^86 * a * x + x^2 - 2^85 * b + c - y
roots = coron(f, X=2^85, Y=2^85, k=1, debug=True)[0]
x, y = roots

改了一下

1
2
3
4
5
6
7
8
9
10
11
p = 92946459607669937513774102250057295249718593723232674702212854287358873135783
Fp = Zmod(p)
pi = 43844336985235863734419631630425915388298791521868754583032904718644333115590
x_ = [3248642833056635029095920782095626337949113592116495266, 4883935221919623989344404485025479346028101682781790392]

P.<t> = PolynomialRing(Fp)
f = t * t + pi

PR.<k> = PolynomialRing(Fp)
s = f(x_[0]*2^73 + k)//2*73-x_[1]
root = s.small_roots(X=2^73, beta=1)[0]

有几个问题，首先这样向右位移不知道中不中，然后总是报越界的错

image-20210711134025217

在尝试以及一些等效替代无果后，我想到再添加一个变量；一是因为这样表示更加清晰，省去了向右位移的不确定性，二是la佬的博客里，也有求解多元多项式的脚本

设 x[0] x[1] 的低73位为 k0 和 k1，写出来的等式是
$$
f(x_{0}<<73+k_0)=x_{1}<<73+k_1\notag
$$
然后找到了原题

是三个月前 zer0pts CTF 的题目，找到了 Joseph 师傅的博客，参考zer0pts CTF 2021 - Crypto-easy pseudo random

然后当时就是改了他的脚本做出来的，除了一些推导，还提供了一个 coppersmith 求小根函数的 github 链接，https://github.com/defund/coppersmith/

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
import itertools

def small_roots(f, bounds, m=1, d=None):
	if not d:
		d = f.degree()

	R = f.base_ring()
	N = R.cardinality()

	f /= f.coefficients().pop(0)
	f = f.change_ring(ZZ)

	G = Sequence([], f.parent())
	for i in range(m+1):
		base = N^(m-i) * f^i
		for shifts in itertools.product(range(d), repeat=f.nvariables()):
			g = base * prod(map(power, f.variables(), shifts))
			G.append(g)

	B, monomials = G.coefficient_matrix()
	monomials = vector(monomials)

	factors = [monomial(*bounds) for monomial in monomials]
	for i, factor in enumerate(factors):
		B.rescale_col(i, factor)

	B = B.dense_matrix().LLL()

	B = B.change_ring(QQ)
	for i, factor in enumerate(factors):
		B.rescale_col(i, 1/factor)

	H = Sequence([], f.parent().change_ring(QQ))
	for h in filter(None, B*monomials):
		H.append(h)
		I = H.ideal()
		if I.dimension() == -1:
			H.pop()
		elif I.dimension() == 0:
			roots = []
			for root in I.variety(ring=ZZ):
				root = tuple(R(root[var]) for var in f.variables())
				roots.append(root)
			return roots

	return []

稍微改一下脚本就出来了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
load('coppersmith.sage')
from Crypto.Util.number import long_to_bytes

p = 92946459607669937513774102250057295249718593723232674702212854287358873135783
Fp = Zmod(p)
b = 43844336985235863734419631630425915388298791521868754583032904718644333115590
c = 193207529097125793778662519051231322609402866155819915933598367395102313904490702547833
w0 = 3248642833056635029095920782095626337949113592116495266
w1 = 4883935221919623989344404485025479346028101682781790392

b,w0,w1 = map(Fp, [b,w0,w1])
PR.<k0, k1> = PolynomialRing(Fp)

f = 2^146 * w0^2 + 2^74 * w0 * k0 + k0^2 - 2^73 * w1 + b - k1
roots = small_roots(f, (2^73, 2^73), m=3)[0]
k0, k1 = roots

v0 = 2^73 * w0 + k0
v1 = 2^73 * w1 + k1

PR.<v> = PolynomialRing(Fp)
f = v^2 + b
y = f(v1)
for i in range(7):
    y = f(y)
    c ^^= int(y)
print(long_to_bytes(c))

将这个函数用到我昨天的等式上，发现也可以出来

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
load("coppersmith.sage")
from Crypto.Util.number import long_to_bytes

p = 92946459607669937513774102250057295249718593723232674702212854287358873135783
Fp = Zmod(p)
pi = 43844336985235863734419631630425915388298791521868754583032904718644333115590
x_ = [3248642833056635029095920782095626337949113592116495266, 4883935221919623989344404485025479346028101682781790392]
c = 193207529097125793778662519051231322609402866155819915933598367395102313904490702547833

PR.<t> = PolynomialRing(Fp)
f = t * t + pi

PR.<k0, k1> = PolynomialRing(Fp)
s = f(x_[0]*2^73 + k0)-x_[1]*2^73-k1
roots = small_roots(s, (2^73, 2^73), m=3)[0]
k0, k1 = roots

v0 = 2^73 * x_[0] + k0
v1 = 2^73 * x_[1] + k1

y = f(v1)
for i in range(7):
    y = f(y)
    c ^^= int(y)
print(long_to_bytes(c))

海那边漂来的漂流瓶

春哥师傅的题目

题目描述

在海的那边漂过来一个漂流瓶，停在了沙滩上。 你把它捡起来，却不知道漂流瓶里的纸上到底写了些啥。

1
ZJ6 -3 AI6 G8 EL NJ4 EJ/ XJ4 1O3 FU3 RU RUP EJ/ XJ4 S06 54 284 Q/6 J0 ， 5J3 VU04 T;6 2J4 431 EJ/ XU3 。 Y4 1O3 D9 G3 S06 VU/6 ， U VM4 RU/ EJI4 RU XJ/6 G4 、 VUP 1O3 G4 、 W96 1O3 G4 、 WL6 M06 G4 、 VUP 5J6 VU04 、 VUP 5J6 G4 、 AUL6 XU4 VU04 、 W96 5J/ G4 、 5; CJ84 VU04 、 S06 W.6 VU04 、 MP6 XUP6 VU04 、 RU8 U4 VU04 、 RU8 U4 G4 、 W96 S06 G4 、 EL VM/6 G4 、 QU/6 2J/ VU04 。 ZJ6 X94 EK6 2U6 SO4 BJ/6 G4 T QJ6 WL6 1J4 WJ3 QJ6 WL6 QU6 1J4 T QJ6 WL6 2L3 WJ3 QJ6 WL6 QU6 2U6 C04 M3 QUP UP G.3 Y4 AJ3 QUP RU, 。 FU6 5J/ U.6 M6 XJ4 2J04 RU04 GK4 G6 2U6 M/4 2U4 FM3 2K6 JP4 WU6 ， Y94 W96 5J/ G4 M3 5; CJ84 VU04 5 RU0 M06 1P3 U/ E9 G4 S06 1O3 Y.3 VU;4 2U6 ZJ6 -3 AI6 G8 EL NJ4 EJ/ XJ4 CP3 XU4 J94 2U4 G4 T/6 VU04 2J/ VU VU;4 2U6 Y.3 VU;4 ， Y4 S06 1J4 1O3 G;4 VU0 RU/ 5; CJ84 VU04 ZP M06 VU; ， DJ84 J VU 54 W96 5J/ G4 J4 Z/ FM 、 J B4 FM 5 C.4 ， Y94 VU;4 VU VU/6 54 5; CJ84 VU04 1O3 1J4 2U6 5; CJ84 G4 ， U06 J VU （ NJ6 T/ 284 2J4 VU ） VU VU/6 54 5; CJ84 VU04 CK6 AO3 5P4 ， 5J03 EK4 RU, RUP4 56 RUL3 2U6 284 J0 ， DJ84 M,4 284 2J4 VU RUP4 BJ4 W96 5J/ G4 C93 VU04 2U4 FM 。 1U,6 J;4 RU4 183 ZJ6 X94 EK6 M/4 VU WU 94 ZJ3 VU.4 2U6 EK6 G4 1L EJI3 FU3 X96 I6 。 VU; 2JO4 M6 5J/ G0 EL 2; TJ EJO CJ86 G4 U3 TJ04 XU06 W96 J0 VU 04 5J3 UL4 284 T/6 G4 JO6 AJ4 2U6 ， DL3 XU;6 2L4 QU/6 C/6 2U4 FM Z8 503 、 WJ3 2U4 FM3 2K6 2U6 T/6 1P3 M3 1U4 AU03 2J G4 ZJ4 RUP4 2J03 WJ6 WJ/ FUP6 TK XU.6 YL4 T/6 YJ3 N9 ， ZJ6 -3 AI6 G8 EL NJ4 EJ/ XJ4 2U6 VM03 VU04 RU, DK4 U4 1U4 D9 1J4 ZP BP6 D.3 T.6 AU4 2U6 2J CJO4 FM 1U/4 RU/ EJI4 VM3 2JI M06 1P3 2U 2J4 D9 Z8 2U6 VU; HJP 2U4 294 。

hint1

1
广州火车站上霸气外露的标语：统一祖国 振兴中华

hint2

1
靠北耶！E04！

解题思路

显然是类似一种单表替换的东西，然后随便挑了几个去搜，就在 github 上找到https://github.com/chinese-opendesktop/cin-tables/blob/master/bopomofo.cin 至于第一个 hint 我到现在都没有理解其意思，第二个 hint 是台湾方言和台湾网络用语

github 里是正体注音輸入法的对照词库吧，正好对应了 E04! 的由来，也很呼应题目

手撕了

1
福尔摩沙高速公路北起基金公路南至大鹏湾，主线长431公里，自北开始南行，依序经过基隆市、台北县、桃园县、新竹县、苗栗县、台中县、彰化县、南投县、云林县、嘉义县、台南县、高雄县与屏东县。fu lai ge的内容是吃葡萄不吐葡萄皮不吃葡萄不吐葡萄皮的汉语拼音首字母拼接。

然后看官方 WP 春哥师傅说可以用在线的网站搞；切换下输入法就好

image-20210711151337886

群主说要出简单的题目大家把这题想简单一点

1
2
3
N = 24873777989291448485268365702265085243886872900039809831478881276969311714448924581398692832639705916538111455861057354225427758736198452679468399039512440497290615485190994957684665065261280544484301856860844163436499302230085760545686486398949018187416289923500558688885485672960734334858119391323987554701544773420070317895909846297195832399677291338220818181502181317849952785959097285626009703863257450199781708945715701136683994546852422993684382468187651935055302074609980311161155531603473091857526099148935429447319415714778860215376802270686310782735079899235228731429165106477537031235405221734008734614847
e = 12436888994645724242634182851132542621943436450019904915739440638484655857224462290699346416319852958269055727930528677112713879368099226339734199519756220248645307742595497478842332532630640272242150928430422081718249651115042880272843243199474509093708144961750279344442742836480367167429059695661993777350613653317802356713323129593521588320771616955563426747034967432053960828426250168954828986666929922730060781213890566121107119389060806644531516491192343284701151238691996162679338542186167193568672632227858449997036747029810933106336313085633759799229646747282205612102678724267585967720538082620536177904609
c = 7539424334663709603622451394173266049480031393220309445902319310504736287365860451132752036622339554159799611768328686792828750952551268647863160547774237934958072391797341405165512721597085695555356929495861914056799039140107261439671707574841789330531198534325422015873621769489969596614802282764401661006564546159674397356683650318142728009273827997179696988926599672213482848150751054351595386402597000601684644207559735499031666361222038615475154046453649719203304187309556004660926226182353445661702352380654352874617084419834338343925880593023307238768452509962

e 很大，尝试过 boneh_durfee，但是出不来；检查条件，这 e 也太大了吧

然后在诸多hint中看到

当你凝视密文的时候，密文也在凝视着你

哈哈

当你凝视密文的时候，明文也在凝视着你

The Dedication of Suspect M

8神师傅的题目，春哥师傅隔了7分钟就出了并且全场唯一解，直到比赛结束，我都丝毫没有头绪

题目描述

题目信息很多

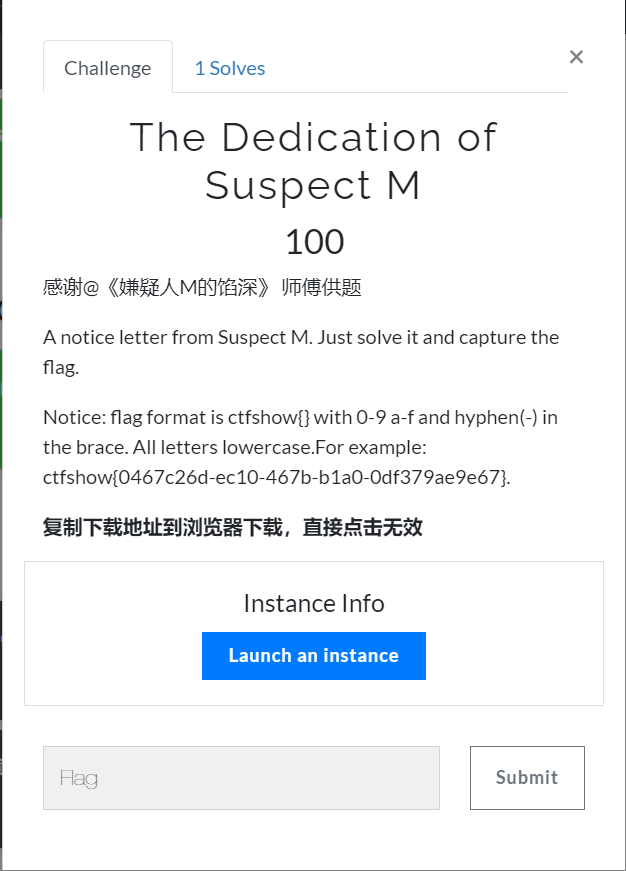
image-20210711152717959

解题思路

我整理出来的，有以下线索：

  • 是一个动态的环境，提供压缩包下载，里面有个名为 M 的二进制文件，文件内容每重开一次环境都不相同、大小从 2K 到 5K 不等；那么flag 基本上也是动态的了

  • flag 的内容是小写字母的十六进制，中间有短横分隔

  • 嫌疑人X的献身改成了嫌疑人M的陷深

根据现有的线索：动态的每次 flag 都不相同、0-9 a-f，我所能想到的就是

image-20210711154007056

但我和组内的师傅试过，不管是给文件 md5，还是给压缩包 md5，都不太行

春哥的思路是将那些不可见的字符给转变成换行符0D 0A，也就是\r \n，windows用\r\n表示换行

就是将这些不可见的小点通过在128个ascii字符表中位移带走

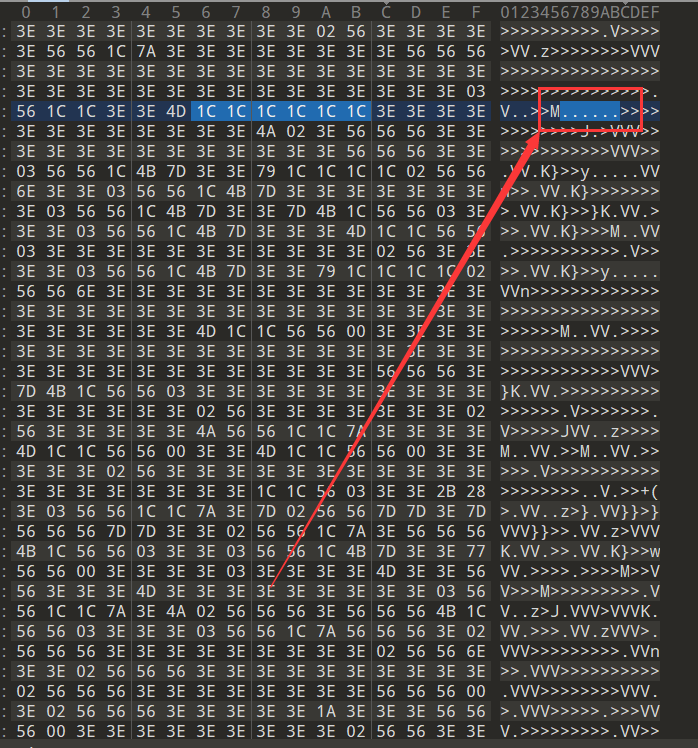
image-20210712094503819

春哥师傅准确计算出了密钥，我第一次也可以，但怎么改那些小字母数字提交的flag都不对，之后我重新开了几次环境，就直接爆破了

1
2
3
4
5
6
7
8
with open('../M', 'rb') as f:
    s = f.read()

for i in range(128):
    t = bytes([(x - i) % 128 for x in s])
    print(t.decode())
    print(i)
    print('''===================================''')

找到像样的，是figlet艺术字，手敲一遍

image-20210712093228438

比赛结束，刷了几道CTFSHOW上的题，记录一下

36D杯

justShow

1
hlcgoyfsjqknyifnpd:bcdefghijklmnopqrstuvwxyza

冒号后面的提示凯撒位移，移回来得到

1
gkbfnxeripjmxhemoc:abcdefghijklmnopqrstuvwxyz

然后没想到是playfair，后面是key；拿去在线网站解密一下

这里有点狗，因为playfair的字母表只有25个，一般是用i代替j；但这里不是，还没有明说，所以缺省情况是出不来的。因为key就是a-z，所以字母表就是a-z，不用代替任何字母了，随便改一下参数

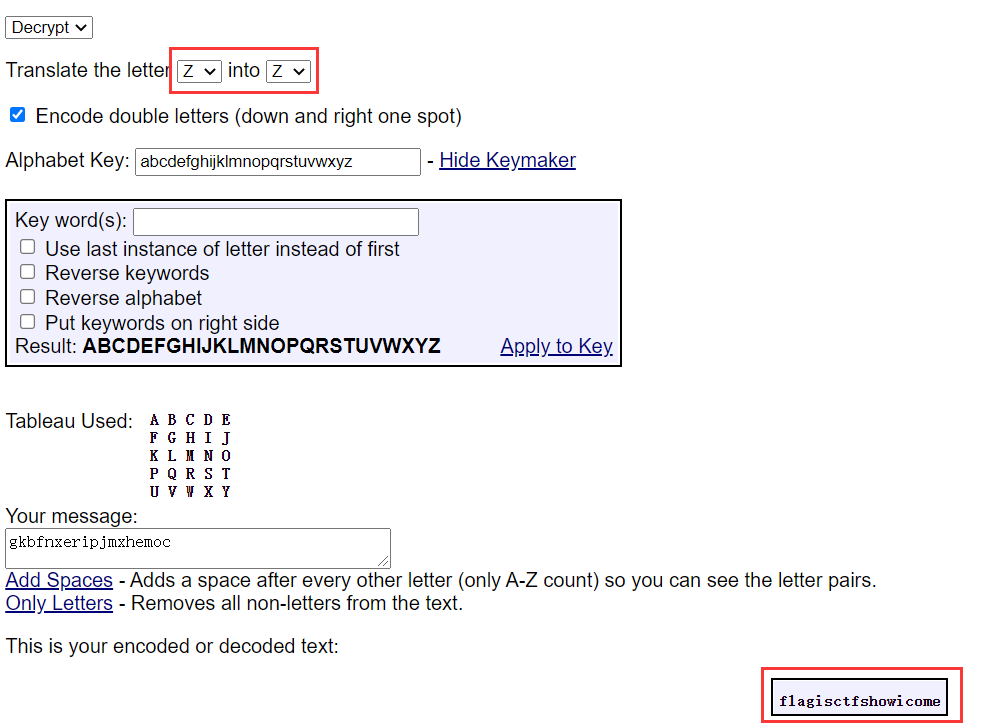
image-20210711101933363

得到flag

1
flagctfshow{ctfshowicome}

飞鸽传书

提供附件下载，pub.key

1
TVdJd09HRm1NamMyWkdKak56VTVNekkzTVdZMFpXVTJNVFl5T0Rrek1qUWxNRUZsTW1GbE0yRXlNelV3TnpRell6VXhObU5rWVRReE1qUTVPV0poTTJKbE9TVXdRV0prWlRVeVkySXpNV1JsTXpObE5EWXlORFZsTURWbVltUmlaRFptWWpJMEpUQkJaVEl6WlRBd1ltVXpPV1F6Tm1Zek5EWXlaVFUzTm1FMk4yRTNaamt4T1RrbE1FRXhPR00zT1RJNE5XSTFNVFJqTmpObVl6a3dNelZsTTJZNU1qQmhaVFEzTnlVd1FXUmhORFJrWkRFNU1tUmxabVF4WW1VM09XWTJNMk16TlRCa01qa3lNR05tSlRCQk5ESTFNV00wWXpZME9XTTNaREptT0RZek1qZGxabVJsTWpNNU9USm1ZVGNsTUVGaFlXVTNZakprTkRneU16Z3lZV0ZoWkRjMVptUmxOalJrWmpobVpqZzJaaVV3UVRJNU5tWTNabVpqTW1VME5UUTFaR00zTnpreU1EVXdZMlZpTkdFNE56RXhKVEJCTmpFd04yRmpNV0UxTldZeFpUQm1aV05pTjJSa1lqWXdabUl6WW1ZeE1Ea2xNRUZoWldNeU16TXpNekl4WkRjek1EQXdNVFl4TmpneVpETmpOR1ZpWXpBd09TVXdRVFV3TURWaU0ySm1NREF3TlRCaVpqUm1OMlUwTTJGak16TmhNRFExTkdJNEpUQkI=

不是很正规的PEM格式的公钥文件，尝试手撕，两次Base64，一次URL，得到

1
2
3
4
5
6
7
8
9
10
11
12
1b08af276dbc7593271f4ee616289324
e2ae3a2350743c516cda412499ba3be9
bde52cb31de33e46245e05fbdbd6fb24
e23e00be39d36f3462e576a67a7f9199
18c79285b514c63fc9035e3f920ae477
da44dd192defd1be79f63c350d2920cf
4251c4c649c7d2f86327efde23992fa7
aae7b2d482382aaad75fde64df8ff86f
296f7ffc2e4545dc7792050ceb4a8711
6107ac1a55f1e0fecb7ddb60fb3bf109
aec2333321d73000161682d3c4ebc009
5005b3bf00050bf4f7e43ac33a0454b8

看着有点像MTP，跑一下美团用过的脚本，出来这样一个玩意，没有任何实际意思可言，麻了

image-20211116183626206

然后看了wp是hash函数类型的，然后找逆hash的网站，有些网站要登录收费了；解成功的几个发现是md4，且结果有数字和字母，于是自己写个爆破一下

记得hashlib库里好像没有md4，就从github上随便找了一段源码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
def _pad(msg):
    n = len(msg)
    bit_len = n * 8
    index = n & 0x3f
    pad_len = 120 - index
    if index < 56:
        pad_len = 56 - index
    padding = b'\x80' + b'\x00' * 63
    suffix = bit_len.to_bytes(8, 'little', signed=False)
    padded_msg = msg + padding[:pad_len] + suffix
    return padded_msg


def _left_rotate(n, b):
    return ((n << b) | ((n & 0xffffffff) >> (32 - b))) & 0xffffffff


def _if(x, y, z):
    return x & y | ~x & z


def _maj(x, y, z):
    return x & y | x & z | y & z


def _xor3(x, y, z):
    return x ^ y ^ z


def _f1(a, b, c, d, k, s, X):
    return _left_rotate(a + _if(b, c, d) + X[k], s)


def _f2(a, b, c, d, k, s, X):
    return _left_rotate(a + _maj(b, c, d) + X[k] + 0x5a827999, s)


def _f3(a, b, c, d, k, s, X):
    return _left_rotate(a + _xor3(b, c, d) + X[k] + 0x6ed9eba1, s)


class MD4:
    def __init__(self):
        self.A = 0x67452301
        self.B = 0xefcdab89
        self.C = 0x98badcfe
        self.D = 0x10325476

    def update(self, message_string):
        msg_bytes = _pad(message_string)
        for i in range(0, len(msg_bytes), 64):
            self._compress(msg_bytes[i:i + 64])

    def _compress(self, block):
        a, b, c, d = self.A, self.B, self.C, self.D

        x = []
        for i in range(0, 64, 4):
            x.append(int.from_bytes(block[i:i + 4], 'little', signed=False))

        a = _f1(a, b, c, d, 0, 3, x)
        d = _f1(d, a, b, c, 1, 7, x)
        c = _f1(c, d, a, b, 2, 11, x)
        b = _f1(b, c, d, a, 3, 19, x)
        a = _f1(a, b, c, d, 4, 3, x)
        d = _f1(d, a, b, c, 5, 7, x)
        c = _f1(c, d, a, b, 6, 11, x)
        b = _f1(b, c, d, a, 7, 19, x)
        a = _f1(a, b, c, d, 8, 3, x)
        d = _f1(d, a, b, c, 9, 7, x)
        c = _f1(c, d, a, b, 10, 11, x)
        b = _f1(b, c, d, a, 11, 19, x)
        a = _f1(a, b, c, d, 12, 3, x)
        d = _f1(d, a, b, c, 13, 7, x)
        c = _f1(c, d, a, b, 14, 11, x)
        b = _f1(b, c, d, a, 15, 19, x)

        a = _f2(a, b, c, d, 0, 3, x)
        d = _f2(d, a, b, c, 4, 5, x)
        c = _f2(c, d, a, b, 8, 9, x)
        b = _f2(b, c, d, a, 12, 13, x)
        a = _f2(a, b, c, d, 1, 3, x)
        d = _f2(d, a, b, c, 5, 5, x)
        c = _f2(c, d, a, b, 9, 9, x)
        b = _f2(b, c, d, a, 13, 13, x)
        a = _f2(a, b, c, d, 2, 3, x)
        d = _f2(d, a, b, c, 6, 5, x)
        c = _f2(c, d, a, b, 10, 9, x)
        b = _f2(b, c, d, a, 14, 13, x)
        a = _f2(a, b, c, d, 3, 3, x)
        d = _f2(d, a, b, c, 7, 5, x)
        c = _f2(c, d, a, b, 11, 9, x)
        b = _f2(b, c, d, a, 15, 13, x)

        a = _f3(a, b, c, d, 0, 3, x)
        d = _f3(d, a, b, c, 8, 9, x)
        c = _f3(c, d, a, b, 4, 11, x)
        b = _f3(b, c, d, a, 12, 15, x)
        a = _f3(a, b, c, d, 2, 3, x)
        d = _f3(d, a, b, c, 10, 9, x)
        c = _f3(c, d, a, b, 6, 11, x)
        b = _f3(b, c, d, a, 14, 15, x)
        a = _f3(a, b, c, d, 1, 3, x)
        d = _f3(d, a, b, c, 9, 9, x)
        c = _f3(c, d, a, b, 5, 11, x)
        b = _f3(b, c, d, a, 13, 15, x)
        a = _f3(a, b, c, d, 3, 3, x)
        d = _f3(d, a, b, c, 11, 9, x)
        c = _f3(c, d, a, b, 7, 11, x)
        b = _f3(b, c, d, a, 15, 15, x)

        # update state
        self.A = (self.A + a) & 0xffffffff
        self.B = (self.B + b) & 0xffffffff
        self.C = (self.C + c) & 0xffffffff
        self.D = (self.D + d) & 0xffffffff

    def digest(self):
        return binascii.hexlify(
            self.A.to_bytes(4, 'little', signed=False) + \
            self.B.to_bytes(4, 'little', signed=False) + \
            self.C.to_bytes(4, 'little', signed=False) + \
            self.D.to_bytes(4, 'little', signed=False)
        ).decode('ascii')

exp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
from sage import MD4
from string import printable

cipher = '''1b08af276dbc7593271f4ee616289324
e2ae3a2350743c516cda412499ba3be9
bde52cb31de33e46245e05fbdbd6fb24
e23e00be39d36f3462e576a67a7f9199
18c79285b514c63fc9035e3f920ae477
da44dd192defd1be79f63c350d2920cf
4251c4c649c7d2f86327efde23992fa7
aae7b2d482382aaad75fde64df8ff86f
296f7ffc2e4545dc7792050ceb4a8711
6107ac1a55f1e0fecb7ddb60fb3bf109
aec2333321d73000161682d3c4ebc009
5005b3bf00050bf4f7e43ac33a0454b8'''

for i in printable:
    m = MD4()
    m.update(i.encode('ascii'))
    t = m.digest()
    if t in cipher:
        cipher = cipher.replace(t, i)

for i in cipher.split():
    print(i, end='')

得到flag

1
flag{36D_me}

以后md4不愁了，此外md4也是32位的

BJDCTF

编码与调制

题目描述

1
密文：2559659965656A9A65656996696965A6695669A9695A699569666A5A6A6569666A59695A69AA696569666AA6

hint

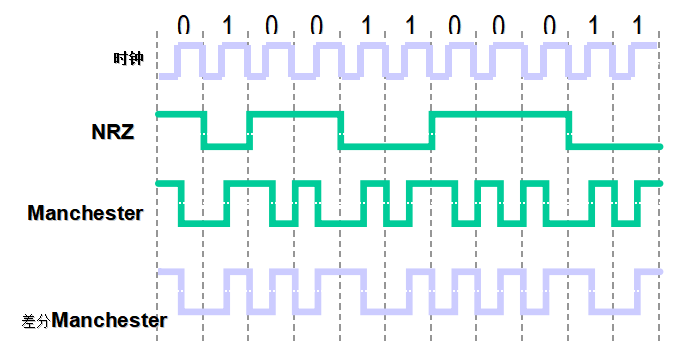
image-20210711162447275

解题思路

计网的知识，曼切斯特和差分曼切斯特

  1. 标准曼切斯特：低到高 0，高到底 1
  2. IEEE曼切斯特：刚好相反，低到高 1，高到底 0
  3. 差分曼切斯特：前后相同为 0，不同为 1
  4. 其他类型：只有5，6，9，a这此种字符的
  5. 注意：存在字节逆序的问题：每8个字节一逆序

老早就在la佬的博客看到，曼切斯特编码的脚本，这次终于用上了，收收好

显然密文中只出现了569a这几个字符，在其他解法这里

image-20210711174323480

这里是省略第一位的，不排除有其他变式，备份一下脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
#!/usr/bin/env python
# -*- coding: utf-8 -*-
import struct
import math


def long_to_bytes(n):
    s = b''
    pack = struct.pack
    while n > 0:
        s = pack('>I', n & 0xffffffff) + s
        n = n >> 32
    for i in range(len(s)):
        if s[i] != b'\000'[0]:
            break
    else:
        s = b'\000'
        i = 0
    s = s[i:]
    return s


# 字节逆序
def byteinvert(str_bin):
    ret = ''
    for i in range(len(str_bin) // 8):
        ret += str_bin[i * 8:i * 8 + 8][::-1]
    return ret


# 标准曼彻斯特
def MCST_stand(str_bin):
    ret = ''
    for i in range(len(str_bin) // 2):
        x = str_bin[i * 2:i * 2 + 2]
        if x == '01':
            ret += '0'
        elif x == '10':
            ret += '1'
        else:
            return 'stand manchester decode wrong!'
    return ret


# IEEE规范的曼彻斯特
def MCST_IEEE(str_bin):
    ret = ''
    for i in range(math.ceil(len(str_bin) / 8)):
        x = str_bin[i * 2:i * 2 + 2]
        if x == '01':
            ret += '1'
        elif x == '10':
            ret += '0'
        else:
            return 'stand manchester decode wrong!'
    return ret


# 差分曼彻斯特
def MCST_diff(str_bin):
    ret = ''
    for i in range(0, len(str_bin) // 2 - 1):
        x1 = str_bin[i * 2:i * 2 + 2]
        x2 = str_bin[i * 2 + 2:i * 2 + 4]
        if x1 == x2:
            ret += '0'
        else:
            ret += '1'
    return ret


if __name__ == "__main__":
    str_hex = '2559659965656A9A65656996696965A6695669A9695A699569666A5A6A6569666A59695A69AA696569666AA6'
    # str_bin='0101010101010101'
    str_bin = str(bin(int(str_hex, 16)))[2:]

    m1 = MCST_IEEE(str_bin)
    m2 = MCST_stand(str_bin)
    m3 = MCST_diff(str_bin)
    print('\nIEEE曼彻斯特:')
    print(m1)
    print(hex(int(m1, 2)))
    print(long_to_bytes(int(m1, 2)))
    print('\n 标准曼彻斯特:')
    print(m2)
    print(hex(int(m2, 2)))
    print(long_to_bytes(int(m2, 2)))
    print('\n 差分曼彻斯特:')
    print(m3)
    print(hex(int(m3, 2)))
    print(long_to_bytes(int(m3, 2)))
    print('\n=============字节逆序=============')
    m1 = byteinvert(m1)
    m2 = byteinvert(m2)
    m3 = byteinvert(m3)
    print('\nIEEE曼彻斯特:')
    print(m1)
    print(hex(int(m1, 2)))
    print(long_to_bytes(int(m1, 2)))
    print('\n 标准曼彻斯特:')
    print(m2)
    print(hex(int(m2, 2)))
    print(long_to_bytes(int(m2, 2)))
    print('\n 差分曼彻斯特:')
    print(m3)
    print(hex(int(m3, 2)))
    print(long_to_bytes(int(m3, 2)))

Polybius

1
密文：ouauuuoooeeaaiaeauieuooeeiea hint：VGhlIGxlbmd0aCBvZiB0aGlzIHBsYWludGV4dDogMTQ=

hint解出来

1
The length of this plaintext: 14

密文全部是由5个元音字母组成，明文的长度是密文的一半，题目提示是是波利比奥斯棋盘密码，没有说密钥

所谓的波利比奥斯棋盘密码，和 playfair 同属于棋盘密码，它用字符表的坐标来代替坐；所以只有1-5，和playfair一样默认用 i 代替 j；这里没有特殊说明，密钥就取这个了

先转成数字，这里第一次犯了迷糊，因为不一定是以 aeiou 的顺序，还需要爆破，这就意味有120种可能；找到了现成的 python 库实现

看一遍就能懂，有一个坑，害我最后直接调试库里的代码才改正，就是这个参数必须给它大写的，不然后面会因为找不到而报错

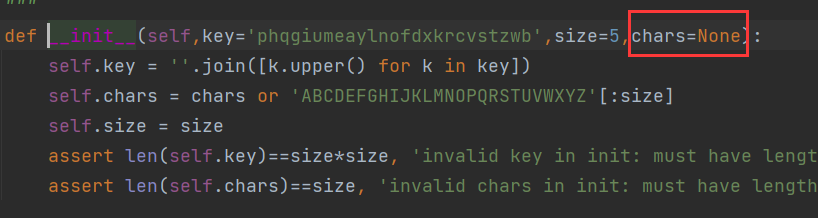
image-20210711190015963

exp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
#!/usr/bin/env python
# -*- coding: utf-8 -*-
from itertools import permutations
from pycipher import PolybiusSquare
from string import ascii_lowercase

square = ascii_lowercase.replace('j', '')
space = 'AEIOU'
cipher = 'ouauuuoooeeaaiaeauieuooeeiea'
for i in permutations(space, 5):
    l = ''.join(list(i))
    p = PolybiusSquare(key=square, size=5, chars=l)
    m = p.decipher(cipher).lower()
    if m.startswith('flag'):
        print(m)

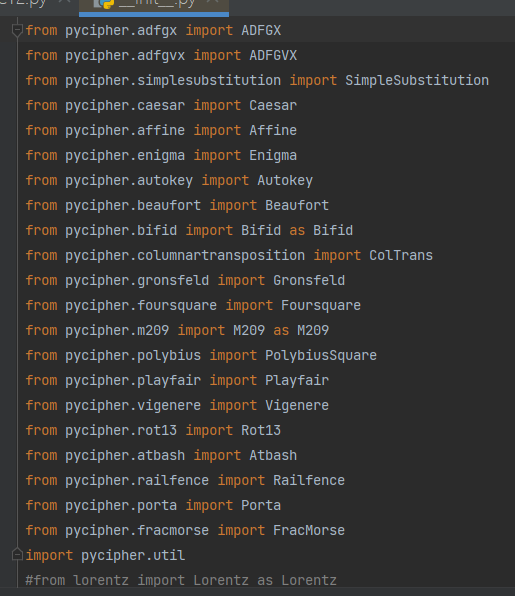
image-20210711190109271

这个库有点东西

密码学AK赛

加法

1
vtu[ypslg;sh}lrunpstf[sddeptf\

冥冥之中很熟悉，但却说不出来是啥加密；本来打算放弃，然后随便抽取一段出来出来搜，发现一篇CSDN的博客，讲的是为了使密码安全，将密码键位向右移动一位，所谓的键位就是在键盘上位置

手撕了

1
cryptoakflag{keyboardpassword}