20210731-DAS & 极客巅峰 & UIUCTF2021 & Cryptoctf-CryptoSecPartWriteUp

Posted on Edited on In , Views: Symbols count in article: 35k Reading time ≈ 32 mins.

 

2021DASCTF实战精英夏令营暨DASCTF July X CBCTF 4th

Crypto-Yusa的密码学签到——BlockTrick

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
from Crypto.Cipher import AES
import os
def pad(a):
	size = (16-len(a)%16)%16
	a += chr(size)*size
	return a

iv = os.urandom(16)
key = os.urandom(16)
enc = AES.new(key,AES.MODE_CBC,iv)
print(iv.encode('hex'))


for _ in range(2):
	try:
		trick = raw_input("")
		trick = pad(trick.decode('hex'))
		cipher = enc.encrypt(trick)
		if trick == cipher and trick != "":
			with open("flag.txt") as f:
				print(f.read())
				exit()
		else:
			print(cipher.encode('hex'))
			print("Try again")
	except:
		exit()

脑洞题，尚师傅给的思路，两轮AES_CBC，用已知IV去异或

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# !/usr/bin/env python
# -*- coding:utf-8 -*-
from pwn import *

context.log_level = 'debug'
sh = remote('node4.buuoj.cn', 25321)
iv = sh.recv()

# first time
sh.send(iv)
cipher = sh.recvline()
sh.recv()

# second time
sh.send(cipher)
sh.recv()

Crypto-Yusa的密码学课堂——SEDSED

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
import os
from My_box import *


def gen_key(key):
    key_64 = ""
    for i in range(16):
        key_64 += '{0:04b}'.format(int(key[i], 16))
    key_56 = gen_56bit(key_64)
    left_key, right_key = key_56[:28], key_56[28:]
    round_keys = list()
    for index in range(2):
        L = circular_shift(left_key, round_shifts[index])
        R = circular_shift(right_key, round_shifts[index])
        round_key = gen_48bit(L + R)
        round_keys.append(round_key)
        left_key = L
        right_key = R
    return round_keys


def circular_shift(key, n):
    temp = ""
    temp = key[n:] + key[:n]
    return temp


def gen_56bit(key):
    key_56 = ""
    for x in KEY_P1:
        key_56 += key[x - 1]
    return key_56


def gen_48bit(key):
    key_48 = ""
    for x in KEY_P2:
        key_48 += key[x - 1]
    return key_48


def encrypt(plain_text, sub_keys):
    plain_textb = ""
    for i in range(16):
        plain_textb += '{0:04b}'.format(int(plain_text[i], 16))

    plain_textp = permutation(plain_textb)
    left, right = plain_textp[:32], plain_textp[32:]
    out = func(right, sub_keys[0])
    temp = int(out, 2) ^ int(left, 2)
    left, right = right, '{0:032b}'.format(temp)
    out = func(right, sub_keys[1])

    temp = int(out, 2) ^ int(left, 2)
    left = '{0:032b}'.format(temp)
    final = inv_permutation(left + right)
    cipher = hex(int(final, 2))[2:]
    return cipher


def permutation(plain_text):
    p = ""
    for x in IP:
        p += plain_text[x - 1]
    return p


def func(text, key):
    exp = expand(text)
    s_input = '{0:048b}'.format(int(exp, 2) ^ int(key, 2))
    s_out = sbox(s_input)
    f_final = per_func(s_out)
    return f_final


def expand(text):
    temp = ""
    for x in E:
        temp += text[x - 1]
    return temp


def inv_permutation(text):
    final = ""
    for x in Inv_IP:
        final += text[x - 1]
    return final


def per_func(s_output):
    s_final = ""
    for x in P:
        s_final += s_output[x - 1]
    return s_final


def sbox(s_input, index=None):
    s_out = ""
    if index != None:
        i = index
        row = int(s_input[0] + s_input[5], 2)
        column = int(s_input[1:5], 2)
        s_out += '{0:04b}'.format(S[i][row][column])
        return s_out
    else:
        for i in range(8):
            row = int(s_input[6 * i] + s_input[6 * i + 5], 2)
            column = int(s_input[6 * i + 1:6 * i + 5], 2)
            s_out += '{0:04b}'.format(S[i][row][column])
        return s_out


def enc(plain_text):
    sub_keys = gen_key(key_64)
    cipher_text = encrypt(plain_text, sub_keys)
    return cipher_text


def pad(plain_text):
    size = (16 - (len(plain_text) % 16)) % 16
    plain_text += size * '0'
    return plain_text


def myenc(plain_text):
    plain_text = pad(plain_text)
    cipher_text = ""
    for i in range(0, len(plain_text), 16):
        block = plain_text[i:i + 16]
        block_enc = enc(block).rjust(16, '0')
        cipher_text += block_enc
    return cipher_text


def enc2(plain_text, key):
    sub_keys = gen_key(key)
    cipher_text = encrypt(plain_text, sub_keys)
    return cipher_text


key_64 = os.urandom(8).hex()

teststring = "testtest"
print(enc2(teststring.encode().hex(), key_64))

with open("flag.txt") as f:
    flag = f.read()

print("flag: ", myenc(flag.encode().hex()))

# 77a35598c47aeea6
# flag:  86721c7c1ebe2d0af8aa8e073073931b4a5ae6dcf03c784e3c70b5f8ce71cf9eb87f9b836eea0118

My_box

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
# 64->56
KEY_P1 = [57, 49, 41, 33, 25, 17, 9, 1, 58, 50, 42, 34, 26, 18, 10, 2, 59, 51, 43, 35, 27, 19, 11, 3, 60, 52, 44, 36,
          63, 55, 47, 39, 31, 23, 15, 7, 62, 54, 46, 38, 30, 22, 14, 6, 61, 53, 45, 37, 29, 21, 13, 5, 28, 20, 12, 4]
round_shifts = [1, 1, 2, 2, 2, 2, 2, 2, 1, 2, 2, 2, 2, 2, 2, 1]
# 56->48
KEY_P2 = [14, 17, 11, 24, 1, 5, 3, 28, 15, 6, 21, 10, 23, 19, 12, 4, 26, 8, 16, 7, 27, 20, 13, 2, 41, 52, 31, 37, 47,
          55, 30, 40, 51, 45, 33, 48, 44, 49, 39, 56, 34, 53, 46, 42, 50, 36, 29, 32]

IP = [58, 50, 42, 34, 26, 18, 10, 2, 60, 52, 44, 36, 28, 20, 12, 4, 62, 54, 46, 38, 30, 22, 14, 6, 64, 56, 48, 40, 32,
      24, 16, 8, 57, 49, 41, 33, 25, 17, 9, 1, 59, 51, 43, 35, 27, 19, 11, 3, 61, 53, 45, 37, 29, 21, 13, 5, 63, 55, 47,
      39, 31, 23, 15, 7]
E = [32, 1, 2, 3, 4, 5, 4, 5, 6, 7, 8, 9, 8, 9, 10, 11, 12, 13, 12, 13, 14, 15, 16, 17, 16, 17, 18, 19, 20, 21, 20, 21,
     22, 23, 24, 25, 24, 25, 26, 27, 28, 29, 28, 29, 30, 31, 32, 1]

S = [
    # Box-1
    [
        [14, 4, 13, 1, 2, 15, 11, 8, 3, 10, 6, 12, 5, 9, 0, 7],
        [0, 15, 7, 4, 14, 2, 13, 1, 10, 6, 12, 11, 9, 5, 3, 8],
        [4, 1, 14, 8, 13, 6, 2, 11, 15, 12, 9, 7, 3, 10, 5, 0],
        [15, 12, 8, 2, 4, 9, 1, 7, 5, 11, 3, 14, 10, 0, 6, 13]
    ],
    # Box-2

    [
        [15, 1, 8, 14, 6, 11, 3, 4, 9, 7, 2, 13, 12, 0, 5, 10],
        [3, 13, 4, 7, 15, 2, 8, 14, 12, 0, 1, 10, 6, 9, 11, 5],
        [0, 14, 7, 11, 10, 4, 13, 1, 5, 8, 12, 6, 9, 3, 2, 15],
        [13, 8, 10, 1, 3, 15, 4, 2, 11, 6, 7, 12, 0, 5, 14, 9]
    ],

    # Box-3

    [
        [10, 0, 9, 14, 6, 3, 15, 5, 1, 13, 12, 7, 11, 4, 2, 8],
        [13, 7, 0, 9, 3, 4, 6, 10, 2, 8, 5, 14, 12, 11, 15, 1],
        [13, 6, 4, 9, 8, 15, 3, 0, 11, 1, 2, 12, 5, 10, 14, 7],
        [1, 10, 13, 0, 6, 9, 8, 7, 4, 15, 14, 3, 11, 5, 2, 12]

    ],

    # Box-4
    [
        [7, 13, 14, 3, 0, 6, 9, 10, 1, 2, 8, 5, 11, 12, 4, 15],
        [13, 8, 11, 5, 6, 15, 0, 3, 4, 7, 2, 12, 1, 10, 14, 9],
        [10, 6, 9, 0, 12, 11, 7, 13, 15, 1, 3, 14, 5, 2, 8, 4],
        [3, 15, 0, 6, 10, 1, 13, 8, 9, 4, 5, 11, 12, 7, 2, 14]
    ],

    # Box-5
    [
        [2, 12, 4, 1, 7, 10, 11, 6, 8, 5, 3, 15, 13, 0, 14, 9],
        [14, 11, 2, 12, 4, 7, 13, 1, 5, 0, 15, 10, 3, 9, 8, 6],
        [4, 2, 1, 11, 10, 13, 7, 8, 15, 9, 12, 5, 6, 3, 0, 14],
        [11, 8, 12, 7, 1, 14, 2, 13, 6, 15, 0, 9, 10, 4, 5, 3]
    ],
    # Box-6

    [
        [12, 1, 10, 15, 9, 2, 6, 8, 0, 13, 3, 4, 14, 7, 5, 11],
        [10, 15, 4, 2, 7, 12, 9, 5, 6, 1, 13, 14, 0, 11, 3, 8],
        [9, 14, 15, 5, 2, 8, 12, 3, 7, 0, 4, 10, 1, 13, 11, 6],
        [4, 3, 2, 12, 9, 5, 15, 10, 11, 14, 1, 7, 6, 0, 8, 13]

    ],
    # Box-7
    [
        [4, 11, 2, 14, 15, 0, 8, 13, 3, 12, 9, 7, 5, 10, 6, 1],
        [13, 0, 11, 7, 4, 9, 1, 10, 14, 3, 5, 12, 2, 15, 8, 6],
        [1, 4, 11, 13, 12, 3, 7, 14, 10, 15, 6, 8, 0, 5, 9, 2],
        [6, 11, 13, 8, 1, 4, 10, 7, 9, 5, 0, 15, 14, 2, 3, 12]
    ],
    # Box-8

    [
        [13, 2, 8, 4, 6, 15, 11, 1, 10, 9, 3, 14, 5, 0, 12, 7],
        [1, 15, 13, 8, 10, 3, 7, 4, 12, 5, 6, 11, 0, 14, 9, 2],
        [7, 11, 4, 1, 9, 12, 14, 2, 0, 6, 10, 13, 15, 3, 5, 8],
        [2, 1, 14, 7, 4, 10, 8, 13, 15, 12, 9, 0, 3, 5, 6, 11]
    ]

]
P = [16, 7, 20, 21, 29, 12, 28, 17, 1, 15, 23, 26, 5, 18, 31, 10, 2, 8, 24, 14, 32, 27, 3, 9, 19, 13, 30, 6, 22, 11, 4,
     25]
Inv_P = [9, 17, 23, 31, 13, 28, 2, 18, 24, 16, 30, 6, 26, 20, 10, 1, 8, 14, 25, 3, 4, 29, 11, 19, 32, 12, 22, 7, 5, 27,
         15, 21]

Inv_IP = [40, 8, 48, 16, 56, 24, 64, 32, 39, 7, 47, 15, 55, 23, 63, 31, 38, 6, 46, 14, 54, 22, 62, 30, 37, 5, 45, 13,
          53, 21, 61, 29, 36, 4, 44, 12, 52, 20, 60, 28, 35, 3, 43, 11, 51, 19, 59, 27, 34, 2, 42, 10, 50, 18, 58, 26,
          33, 1, 41, 9, 49, 17, 57, 25]


def inverse_table(table):
    new = list()
    for x in range(len(table)):
        if (x + 1) in table:
            num = table.index(x + 1) + 1
            new.append(num)
        else:
            new.append(x)
    return new

复现了下DES的流程

des

整道题的思路就是用一组随机的key去加密了已知的testtest得到结果77a35598c47aeea6，并用相同的key去加密我们的flag；那么解题的思路也很明了了，通过已知的明密文设法得到key，然后写解密函数，最终返回到

先搞key1（图中的key1我随便写的），只需要关注上面那个feistel结构

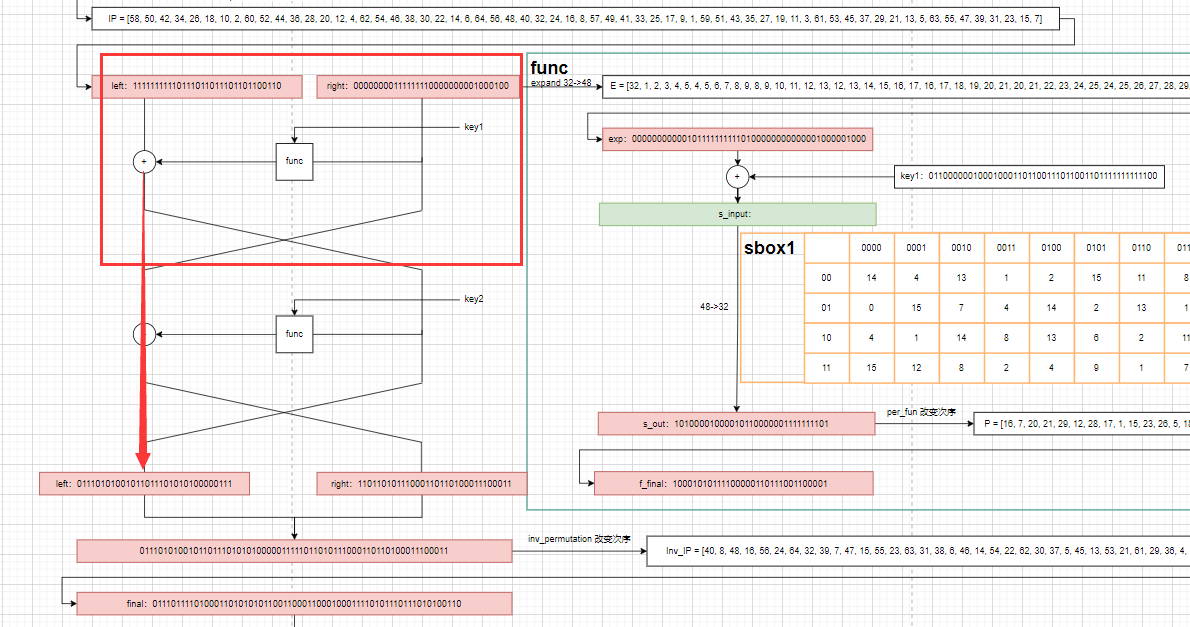
image-20210820190413902

有些是可以直接逆回去的部分，形如inv_permutation和per_func这两个函数，就可以这样逆回来，写的有点臭屁

1
2
3
4
5
6
7
8
9
10
11
12
def inv_permutation(text):
    final = ""
    for x in Inv_IP:
        final += text[x - 1]
    return final


def per_func(s_output):
    s_final = ""
    for x in P:
        s_final += s_output[x - 1]
    return s_final
1
2
3
4
5
6
7
8
9
null = ['' for _ in range(64)]


def permutation(plain_text):
    assert len(plain_text) == len(Inv_IP)
    final = null
    for x in range(len(Inv_IP)):
        final[Inv_IP[x]-1] = plain_text[x]
    return ''.join(final)

然后本题最为关键的就是爆破这个sbox；关于sbox的工作原理，简单来说就是将48位转成32位，中间是每6位转8位，就如wiki百科上以sbox5为例，011011首尾是01，中间是1101，也就是对应坐标1,13，对应到沙盒（这个是可以查表的）就是1001。这样一顿操作下来，就把原来总长48位的，拆分成8个小组，每组6位变成4位，从而最后的总长度为32。显然这个过程是不可逆的

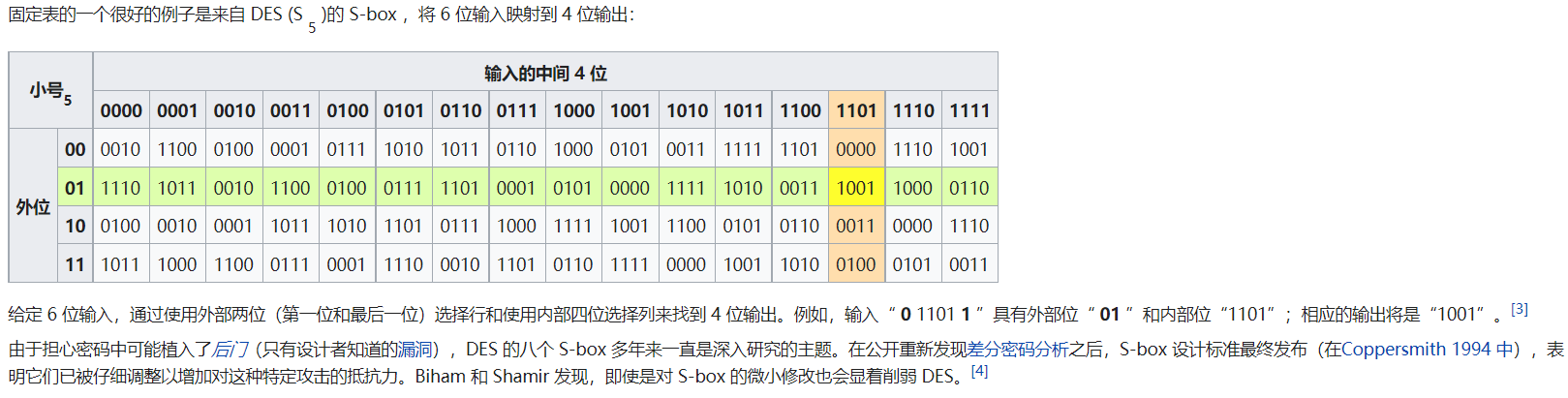
image-20210820204757956

仔细观察沙盒发现一行中是0~15这16个数字打乱顺序，所以一个沙盒要爆破4种情况

写了下脚本，可能有点问题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
#!/usr/bin/env python
# -*- coding: utf-8 -*-
from My_box import *
import sys
from Crypto.Util.number import long_to_bytes

teststring = "testtest"
cipher = 0x77a35598c47aeea6
final = bin(cipher)[2:].rjust(64, '0')
c = '86721c7c1ebe2d0af8aa8e073073931b4a5ae6dcf03c784e3c70b5f8ce71cf9eb87f9b836eea0118'

null64 = ['' for _ in range(64)]
null32 = ['' for _ in range(32)]


def my_permutation(plain_text):
    assert len(plain_text) == len(Inv_IP)
    per_final = null64
    for x in range(len(Inv_IP)):
        per_final[Inv_IP[x]-1] = plain_text[x]
    return ''.join(per_final)


def expand(text):
    temp = ""
    for x in E:
        temp += text[x - 1]
    return temp


def inv_per_func(s_final):
    assert len(s_final) == len(P)
    s_output = null32
    for x in range(len(P)):
        s_output[P[x] - 1] = s_final[x]
    return ''.join(s_output)


def func(text):
    exp = expand(text)
    return exp


def find_column(num, index, row):
    for find_j in range(16):
        if S[index][row][find_j] == num:
            return find_j


def permutation(plain_text):
    p = ""
    for x in IP:
        p += plain_text[x - 1]
    return p


def encrypt(plain_text):
    plain_textb = ""
    for en_i in range(16):
        plain_textb += '{0:04b}'.format(int(plain_text[en_i], 16))
    plain_textp = permutation(plain_textb)
    en_left, en_right = plain_textp[:32], plain_textp[32:]
    out = func(en_right)
    return en_left, en_right, out


def sbox(s_input):
    s_out = ''
    for sbox_i in range(8):
        s_row = int(s_input[6 * sbox_i] + s_input[6 * sbox_i + 5], 2)
        s_column = int(s_input[6 * sbox_i + 1:6 * sbox_i + 5], 2)
        s_out += '{0:04b}'.format(S[sbox_i][s_row][s_column])
    return s_out


def per_func(s_output):
    s_final = ""
    for x in P:
        s_final += s_output[x - 1]
    return s_final


def inv_permutation(cipher_text):
    assert len(cipher_text) == len(IP)
    p = null64
    for x in range(len(IP)):
        p[IP[x] - 1] = cipher_text[x]
    return ''.join(p)


def decrypt(cipher_text, d_sub_keys):
    d_final = bin(int(cipher_text, 16))[2:].rjust(64, '0')
    d_final = my_permutation(d_final)
    d_left, d_right = d_final[:32], d_final[32:]
    # RIGHT
    d_EXP = func(d_left)
    # inv_func
    d_s_input = '{0:048b}'.format(int(d_EXP, 2) ^ int(d_sub_keys[1], 2))
    d_s_out = sbox(d_s_input)
    out = per_func(d_s_out)

    d_RIGHT = bin(int(out, 2) ^ int(d_right, 2))[2:].rjust(32, '0')

    # LEFT
    d_EXP = func(d_RIGHT)
    d_s_input = '{0:048b}'.format(int(d_EXP, 2) ^ int(d_sub_keys[0], 2))
    d_s_out = sbox(d_s_input)
    out = per_func(d_s_out)

    d_LEFT = bin(int(out, 2) ^ int(d_left, 2))[2:].rjust(32, '0')
    plaintext = d_LEFT + d_RIGHT
    plaintext = inv_permutation(plaintext)
    plaintext = ''.join(hex(int(plaintext[_:_+4], 2))[2:] for _ in range(0, len(plaintext), 4))
    return plaintext


def inv_rjust(cipher_text):
    for rjust_i in range(len(cipher_text)):
        if cipher_text[rjust_i] != '0':
            return cipher_text[rjust_i:]


def inv_pad(cipher_text):
    for pad_i in range(len(cipher_text)-1, -1, -1):
        if cipher_text[pad_i] != '0':
            return cipher_text[:pad_i]


def mydec(ciphertext, d_sub_keys):
    plaintext = ''
    for de_i in range(0, len(ciphertext), 16):
        block_enc = inv_rjust(ciphertext[de_i:de_i + 16])
        block = decrypt(block_enc, d_sub_keys)
        plaintext += block
    plaintext = inv_pad(plaintext)
    return plaintext


LEFT, RIGHT, EXP1 = encrypt(teststring.encode().hex())
final = my_permutation(final)
left, right = final[:32], final[32:]
EXP2 = func(left)

# key1
f_final1 = bin(int(left, 2) ^ int(LEFT, 2))[2:].rjust(32, '0')
# inv_func
s_out1 = inv_per_func(f_final1)
# inv_sbox
for i in range(65536):
    bin_i = bin(i)[2:].rjust(16, '0')
    a1 = [int(bin_i[_]+bin_i[_+1], 2) for _ in range(0, len(bin_i), 2)]
    # j's sbox
    j1 = 0
    # i's row
    s_input1 = ''
    for i1 in a1:
        t1 = int(s_out1[i1 * 4:i1 * 4 + 4], 2)
        column1 = find_column(t1, j1, i1)
        j1 += 1
        s_input1 += bin(i1)[2:].rjust(2, '0')[0] + bin(column1)[2:].rjust(4, '0') + bin(i1)[2:].rjust(2, '0')[-1]
    key1 = bin(int(s_input1, 2) ^ int(EXP1, 2))[2:].rjust(48, '0')
    # key2
    f_final2 = bin(int(right, 2) ^ int(RIGHT, 2))[2:].rjust(32, '0')
    s_out2 = inv_per_func(f_final2)
    for j in range(65536):
        bin_j = bin(j)[2:].rjust(16, '0')
        a2 = [int(bin_j[_] + bin_j[_ + 1], 2) for _ in range(0, len(bin_j), 2)]
        j2 = 0
        s_input2 = ''
        for i2 in a2:
            t2 = int(s_out2[j2 * 4:j2 * 4 + 4], 2)
            column2 = find_column(t2, j2, i2)
            j2 += 1
            s_input2 += bin(i2)[2:].rjust(2, '0')[0] + bin(column2)[2:].rjust(4, '0') + bin(i2)[2:].rjust(2, '0')[-1]
        key2 = bin(int(s_input2, 2) ^ int(EXP2, 2))[2:].rjust(48, '0')
        sub_keys = [key1, key2]
        flag = long_to_bytes(int(mydec(c, sub_keys), 16))
        print(i, i*j)
        if b'flag' in flag:
            print(flag)
            sys.exit(0)

Misc-red_vs_blue

Misc的签到题

给了一个nc，连上玩一下就知道是两种情况让你猜，连续猜对66次得flag，每次连nc输赢的结果不同

写了个脚本，但是有些交互的问题，总之还是一句话一句话接收吧

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
#!/usr/bin/env python
# -*- coding: utf-8 -*-
from pwn import *


def rest():
    # not so fast
    time.sleep(.05)


context.log_level = 'debug'

res = []
r = b'r'
b = b'b'
sh = remote('node4.buuoj.cn', 28719)

# begin info
sh.recv()
while 1:
    # classical try red one
    rest()
    bug = sh.sendline(r)
    feedback = sh.recv()
    if b'Sorry' in feedback:
        res.append(b)
        sh.sendline(b'y')
    else:
        res.append(r)
        continue
    sh.recv()
    for i in res:
        rest()
        sh.sendline(i)
        flag = sh.recv()
        if b'flag' in flag:
            print(flag)
            sh.close()
            break
    print(len(res))

极客巅峰

Crypto-crtrsa

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
from secret import flagn,p,q
#p and q are two primes generated by getPrime
import random
def key_gen():
	while True:
		dp = random.randint(1,1<<20)
		dq = random.randint(1,q-1)
		if gcd(dp, p - 1) == 1 and gcd(dq, q - 1) == 1:
			d = crt([dp,dq],[p-1,q-1])
			phi = (p-1)*(q-1)
			R = Integers(phi)
			e = R(d)^-1
			return p*q,e
n,e = key_gen()
print(e)
print(n)
print(pow(flagn,int(e),n))
1
2
3
e = 2953544268002866703872076551930953722572317122777861299293407053391808199220655289235983088986372630141821049118015752017412642148934113723174855236142887
N = 6006128121276172470274143101473619963750725942458450119252491144009018469845917986523007748831362674341219814935241703026024431390531323127620970750816983
flag = 4082777468662493175049853412968913980472986215497247773911290709560282223053863513029985115855416847643274608394467813391117463817805000754191093158289399

e很大，但是显然d也很大；从已知看，像dp泄漏，但e太大，枚举不了；最后看到RSA - Small CRT Private Exponents

没找到代码，看不懂论文（feiwu

用RsaCtfTool中的一个工具small_crt_exp，参考https://github.com/Ganapati/RsaCtfTool，直接把脚本拿来改了下，exp如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
362
363
364
365
366
367
368
369
370
371
372
373
374
375
376
377
378
379
380
381
382
383
384
385
386
387
388
389
390
391
392
# sage
from sage.libs.ntl.ntl_ZZ_pX import ntl_ZZ_pContext, ntl_ZZ_pX
from functools import reduce
import binascii
import math
import logging
import random

logger = logging.getLogger("global_logger")

try:
    import gmpy2 as gmpy

    gmpy_version = 2
    mpz = gmpy.mpz
    logger.info("[+] Using gmpy version 2 for math.")
except ImportError:
    try:
        import gmpy

        gmpy_version = 1
        mpz = gmpy.mpz
        logger.info("[+] Using gmpy version 1 for math.")
    except ImportError:
        gmpy_version = 0
        mpz = int
        gmpy = None
        logger.info("[+] Using python native functions for math.")


def getpubkeysz(n):
    size = int(math.log2(n))
    if size & 1 != 0:
        size += 1
    return size


def _gcdext(a, b):
    if a == 0:
        return [b, 0, 1]
    else:
        d = b // a
        r = b - (d * a)
        g, y, x = _gcdext(r, a)
        return [g, x - d * y, y]


def _isqrt(n):
    if n == 0:
        return 0
    x, y = n, (n + 1) >> 1
    while y < x:
        x, y = y, (y + n // y) >> 1
    return x


def _gcd(a, b):
    while b:
        a, b = b, a % b
    return abs(a)


def _introot(n, r=2):
    if n < 0:
        return None if r & 1 == 0 else -_introot(-n, r)
    if n < 2:
        return n
    if r == 2:
        return _isqrt(n)
    lower, upper = 0, n
    while lower != upper - 1:
        mid = (lower + upper) >> 1
        m = pow(mid, r)
        if m == n:
            return mid
        elif m < n:
            lower = mid
        elif m > n:
            upper = mid
    return lower


def _introot_gmpy(n, r=2):
    if n < 0:
        return None if r & 1 == 0 else -_introot_gmpy(-n, r)
    return gmpy.root(n, r)[0]


def _introot_gmpy2(n, r=2):
    if n < 0:
        return None if r & 1 == 0 else -_introot_gmpy2(-n, r)
    return gmpy.iroot(n, r)[0]


def _invmod(a, m):
    a, x, u = a % m, 0, 1
    while a:
        x, u, m, a = u, x - (m // a) * u, a, m % a
    return x


def _is_square(n):
    i = _isqrt(n)
    return i ** 2 == n


def miller_rabin(n, k=40):
    # Taken from https://gist.github.com/Ayrx/5884790
    # Implementation uses the Miller-Rabin Primality Test
    # The optimal number of rounds for this test is 40
    # See http://stackoverflow.com/questions/6325576/how-many-iterations-of-rabin-miller-should-i-use-for-cryptographic-safe-primes
    # for justification

    # If number is even, it's a composite number

    if n == 2:
        return True

    if n & 1 == 0:
        return False

    r, s = 0, n - 1
    while s & 1 == 0:
        r += 1
        s >>= 1
    i = 0
    for i in range(0, k):
        a = random.randrange(2, n - 1)
        x = pow(a, s, n)
        if x == 1 or x == n - 1:
            continue
        j = 0
        while j <= r - 1:
            x = pow(x, 2, n)
            if x == n - 1:
                break
            j += 1
        else:
            return False
    return True


def _fermat_prime_criterion(n, b=2):
    """Fermat's prime criterion
    Returns False if n is definitely composite, True if posible prime."""
    return pow(b, n - 1, n) == 1


def _is_prime(n):
    """
    If fermats prime criterion is false by short circuit we dont need to keep testing bases, so we return false for a guaranteed composite.
    Otherwise we keep trying with primes 3 and 5 as base. The sweet spot is primes 2,3,5, it doesn't improvee the runing time adding more primes to test as base.
    If all the previus tests pass then we try with rabin miller.
    All the tests are probabilistic.
    """
    if (
        _fermat_prime_criterion(n)
        and _fermat_prime_criterion(n, b=3)
        and _fermat_prime_criterion(n, b=5)
    ):
        return miller_rabin(n)
    else:
        return False


def _next_prime(n):
    while True:
        if _is_prime(n):
            return n
        n += 1


def erathostenes_sieve(n):
    """ Returns  a list of primes < n """
    sieve = [True] * n
    for i in range(3, isqrt(n) + 1, 2):
        if sieve[i]:
            sieve[pow(i, 2) :: (i << 1)] = [False] * (
                (n - pow(i, 2) - 1) // (i << 1) + 1
            )
    return [2] + [i for i in range(3, n, 2) if sieve[i]]


_primes = erathostenes_sieve


def _primes_yield(n):
    p = i = 1
    while i <= n:
        p = next_prime(p)
        yield p
        i += 1


def _primes_yield_gmpy(n):
    p = i = 1
    while i <= n:
        p = gmpy.next_prime(p)
        yield p
        i += 1


def _primes_gmpy(n):
    return list(_primes_yield_gmpy(n))


def _fib(n):
    a, b = 0, 1
    i = 0
    while i <= n:
        a, b = b, a + b
        i += 1
    return a


def _invert(a, b):
    return pow(a, b - 2, b)


def _lcm(x, y):
    return (x * y) // _gcd(x, y)


def _ilog2_gmpy(n):
    return int(gmpy.log2(n))


def _ilog_gmpy(n):
    return int(gmpy.log(n))


def _ilog2_math(n):
    return int(math.log2(n))


def _ilog_math(n):
    return int(math.log(n))


def _ilog10_math(n):
    return int(math.log10(n))


def _ilog10_gmpy(n):
    return int(gmpy.log10(n))


def _mod(a, b):
    return a % b


if gmpy_version > 0:
    gcd = gmpy.gcd
    invmod = gmpy.invert
    gcdext = gmpy.gcdext
    is_square = gmpy.is_square
    next_prime = gmpy.next_prime
    is_prime = gmpy.is_prime
    fib = gmpy.fib
    primes = _primes_gmpy
    lcm = gmpy.lcm
    invert = gmpy.invert
    powmod = gmpy.powmod
    ilog = _ilog_gmpy
    ilog2 = _ilog2_gmpy
    mod = gmpy.f_mod
    log = gmpy.log
    log2 = gmpy.log2
    log10 = gmpy.log10
    ilog10 = _ilog10_gmpy
    if gmpy_version == 2:
        isqrt = gmpy.isqrt
        introot = _introot_gmpy2
    else:
        isqrt = gmpy.sqrt
        introot = _introot_gmpy
else:
    gcd = _gcd
    isqrt = _isqrt
    introot = _introot
    invmod = _invmod
    gcdext = _gcdext
    is_square = _is_square
    next_prime = _next_prime
    fib = _fib
    primes = erathostenes_sieve
    is_prime = _is_prime
    fib = _fib
    primes = _primes
    lcm = _lcm
    invert = _invmod
    powmod = pow
    ilog = _ilog_math
    ilog2 = _ilog2_math
    mod = _mod
    log = math.log
    log2 = math.log2
    log10 = math.log10
    ilog10 = _ilog10_math


def trivial_factorization_with_n_phi(N, phi):
    m = N - phi + 1
    i = isqrt(pow(m, 2) - (N << 2))  # same as isqrt((m**2) - (4*n))
    roots = int((m - i) >> 1), int((m + i) >> 1)
    if roots[0] * roots[1] == N:
        return roots


__all__ = [
    getpubkeysz,
    gcd,
    isqrt,
    introot,
    invmod,
    gcdext,
    is_square,
    next_prime,
    is_prime,
    fib,
    primes,
    lcm,
    invert,
    powmod,
    ilog2,
    ilog,
    ilog10,
    mod,
    log,
    log2,
    log10,
    trivial_factorization_with_n_phi,
]


def poly_fast_ntl(ctx, f, xs):
    # Fast multipoint evaulation from Modern Computer Algebra 3rd edition 10.1
    n = len(xs)
    rems = [0] * (4 * n)  # segment tree max size

    def build_tree(i, l, r):
        if l + 1 == r:
            x = xs[l] if l < len(xs) else 0
            rems[i] = ntl_ZZ_pX([-x, 1], ctx)
            return
        mid = (l + r) >> 1
        build_tree(i * 2, l, mid)
        build_tree(i * 2 + 1, mid, r)
        rems[i] = rems[i * 2] * rems[i * 2 + 1]

    build_tree(1, 0, n)

    def compute(f, i, l, r):
        if l + 1 == r:
            yield f % rems[i]
            return
        mid = (l + r) >> 1
        yield from compute(f % rems[2 * i], 2 * i, l, mid)
        yield from compute(f % rems[2 * i + 1], 2 * i + 1, mid, r)

    return map(lambda r: Integer(r.list()[0]), compute(f, 1, 0, n))


def factor(n, e, bound):
    # https://mathoverflow.net/questions/120160/attack-on-crt-rsa
    D = ceil(sqrt(bound))
    ctx = ntl_ZZ_pContext(n)  # NTL's polynomial multiplication is much faster
    x = randint(1, n - 1)
    xe = int(powmod(x, e, n))
    poly_factors = []
    for a in range(0, D):
        poly_factors.append(ntl_ZZ_pX([-x, power_mod(xe, a, n)], ctx))
    poly = product(poly_factors)
    xed = int(powmod(xe, D, n))
    ys = [int(powmod(xed, b, n)) for b in range(0, D)]
    for t in poly_fast_ntl(ctx, poly, ys):
        p = gcd(t, n)
        if p > 1 and p < n:
            return p, n // p


if __name__ == "__main__":
    n = 6006128121276172470274143101473619963750725942458450119252491144009018469845917986523007748831362674341219814935241703026024431390531323127620970750816983
    e = 2953544268002866703872076551930953722572317122777861299293407053391808199220655289235983088986372630141821049118015752017412642148934113723174855236142887
    bound = 2**20  # upper bound of min(d_p, d_q)
    for _ in range(3):  # Retrying
        r = factor(n, e, bound)
        if r is not None:
            p, q = r
            print(p)
            exit()
    print(0)  # Prints 0 if failed

用这个可以分解出p

来自天命团队的密码师傅直接推导出来，从dp这个可以爆破点入手，求出了p，强。参考天命团队wp

Crypto-MedicalImage

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
from PIL import Image
from decimal import *
import numpy as np
import random
getcontext().prec = 20

def f1(x):
    # It is based on logistic map in chaotic systems
    # The parameter r takes the largest legal value
    assert(x>=0)
    assert(x<=1)
    ...

def f2(x):
    # same as f1
    ...
def f3(x):
    # same as f1
    ...

def encryptImage(path):
    im = Image.open(path)
    size = im.size
    pic  = np.array(im) 
    im.close()
    r1 = Decimal('0.478706063089473894123')
    r2 = Decimal('0.613494245341234672318')
    r3 = Decimal('0.946365754637812381837')
    w,h = size
    for i in range(200):
        r1 = f1(r1)
        r2 = f2(r2)
        r3 = f3(r3)
    const = 10**14
    for x in range(w):
        for y in range(h):
            x1 = int(round(const*r1))%w
            y1 = int(round(const*r2))%h
            r1 = f1(r1)
            r2 = f2(r2)
            tmp = pic[y,x]
            pic[y,x] = pic[y1,x1]
            pic[y1,x1] = tmp
    p0 = random.randint(100,104)
    c0 = random.randint(200,204)
    config = (p0,c0)
    for x in range(w):
        for y in range(h):
            k = int(round(const*r3))%256
            k = bin(k)[2:].ljust(8,'0')
            k = int(k[p0%8:]+k[:p0%8],2)
            r3 = f3(r3)
            p0 = pic[y,x]
            c0 = k^((k+p0)%256)^c0
            pic[y,x] = c0

    return pic,size,config
def outputImage(path,pic,size):
    im = Image.new('P', size,'white')
    pixels = im.load()
    for i in range(im.size[0]):
        for j in range(im.size[1]):
            pixels[i,j] = (int(pic[j][i]))

    im.save(path)


def decryptImage(pic,size,config):
    .....
    
enc_img = 'flag.bmp'
out_im = 'flag_enc.bmp'

pic,size,_ = encryptImage(enc_img)
outputImage(out_im,pic,size)

不知道为什么没有出，找到混淆函数，然后加密和解密很类似，最后跑了6400张图片，没有解出来

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
#!/usr/bin/env python
# -*- coding: utf-8 -*-
from PIL import Image
from decimal import *
import numpy as np
getcontext().prec = 20
enc_img = 'flag.bmp'
out_im = 'flag_enc.bmp'


def f1(x):
    # It is based on logistic map in chaotic systems
    # The parameter r takes the largest legal value
    x = 4 * x * (1-x)
    assert(x >= 0)
    assert(x <= 1)
    return x


def outputImage(path, pic, size):
    im = Image.new('P', size, 'white')
    pixels = im.load()
    for i in range(im.size[0]):
        for j in range(im.size[1]):
            pixels[i, j] = (int(pic[j][i]))

    im.save(path)


def decryptImage(p1, config, p0x):
    im = Image.open(out_im)
    size = im.size
    pic = np.array(im)
    im.close()
    r1 = Decimal('0.478706063089473894123')
    r2 = Decimal('0.613494245341234672318')
    r3 = Decimal('0.946365754637812381837')
    w, h = size
    rx1 = []
    rx2 = []
    rx3 = []
    for i in range(200):
        r1 = f1(r1)
        r2 = f1(r2)
        r3 = f1(r3)
        rx1.append(r1)
        rx2.append(r2)
        rx3.append(r3)
    for x in range(w-1, -1, -1):
        for y in range(h-1, -1, -1):
            r1 = f1(r1)
            r2 = f1(r2)
            r3 = f1(r3)
            rx1.append(r1)
            rx2.append(r2)
            rx3.append(r3)
    const = 10 ** 14
    p0, c0 = config
    for x in range(w-1, -1, -1):
        for y in range(h-1, -1, -1):
            k = int(round(const * r3)) % 256
            k = bin(k)[2:].ljust(8, '0')
            k = int(k[p0 % 8:] + k[:p0 % 8], 2)
            rx3.pop()
            r3 = rx3[-1]
            p0 = p0x
            c0 = k^((k+p0)%256)^c0
            pic[y, x] = c0
    for x in range(w-1, -1, -1):
        for y in range(h-1, -1, -1):
            x1 = int(round(const * r1)) % w
            y1 = int(round(const * r2)) % h
            rx1.pop()
            rx2.pop()
            r1 = rx1[-1]
            r2 = rx2[-1]
            tmp = pic[y, x]
            pic[y, x] = pic[y1, x1]
            pic[y1, x1] = tmp
    outputImage(p1, pic, size)

i = 1
for p0 in range(100, 105):
    for c0 in range(200, 205):
        for p0xx in range(0, 256):
            decryptImage(str(i)+'.bmp', (p0, c0), p0xx)
            i += 1

看了来自天命团队的WP，还是逆算法的问题，想太简单了，以为加密即解密，稍微改一下就行

摆出re的态度，先cp下源码，自己重新写下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
from PIL import Image
from decimal import *
import numpy as np
import random

getcontext().prec = 20


def f1(x):
    assert (x >= 0)
    assert (x <= 1)
    return 4 * x * (1 - x)


def f2(x):
    assert (x >= 0)
    assert (x <= 1)
    return 4 * x * (1 - x)


def f3(x):
    assert (x >= 0)
    assert (x <= 1)
    return 4 * x * (1 - x)


im = Image.open('flag_enc.bmp')
size = im.size
pic = np.array(im)
im.close()
r1 = Decimal('0.478706063089473894123')
r2 = Decimal('0.613494245341234672318')
r3 = Decimal('0.946365754637812381837')
w, h = size
for i in range(200):
    r1 = f1(r1)
    r2 = f2(r2)
    r3 = f3(r3)
const = 10 ** 14
p = [100, 101, 102, 103]
c = [200, 201, 202, 203]
R1, R2, R3 = r1, r2, r3
l1 = []
l2 = []
for i in range(w * h):
    l1.append(r1)
    l2.append(r2)
    r1 = f1(r1)
    r2 = f2(r2)


def decrypt(p0, c0, r1=R1, r2=R2, r3=R3):
    for x in range(w):
        for y in range(h):
            k = int(round(const * r3)) % 256
            k = bin(k)[2:].ljust(8, '0')
            k = int(k[p0 % 8:] + k[:p0 % 8], 2)
            r3 = f3(r3)
            pic[y, x] = ((pic[y, x] ^ c0 ^ k) - k) % 256
            p0 = pic[y, x]
            c0 = k ^ ((k + p0) % 256) ^ c0
    t = w * h - 1
    for x in range(w - 1, -1, -1):
        for y in range(h - 1, -1, -1):
            x1 = int(round(const * l1[t])) % w
            y1 = int(round(const * l2[t])) % h
            tmp = pic[y, x]
            pic[y, x] = pic[y1, x1]
            pic[y1, x1] = tmp
            t -= 1
    return pic, size


enc_img = 'flag.bmp'
count = 0
for p0 in p:
    for c0 in c:
        pic, size = decrypt(p0, c0)
        im = Image.new('P', size, 'white')
        pixels = im.load()
        for i in range(im.size[0]):
            for j in range(im.size[1]):
                pixels[i, j] = (int(pic[j][i]))
        count += 1
        im.save(str(count) + enc_img)

然后我怎么也想不到会死在这里

image-20210805191752700

运算优先级，异或没有加括号，位运算的优先级比加减要低

顺带发现师傅只爆破了16种情况

我出来是25张flag

image-20210805192547584

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
#!/usr/bin/env python
# -*- coding: utf-8 -*-
from PIL import Image
from decimal import *
import numpy as np
getcontext().prec = 20


def f1(x):
    # It is based on logistic map in chaotic systems
    # The parameter r takes the largest legal value
    assert (x >= 0)
    assert (x <= 1)
    x = 4 * x * (1 - x)
    return x


def f2(x):
    # same as f1
    return f1(x)


def f3(x):
    # same as f1
    return f1(x)


def outputImage(path, pic, size):
    im = Image.new('P', size,'white')
    pixels = im.load()
    for i in range(im.size[0]):
        for j in range(im.size[1]):
            pixels[i, j] = (int(pic[j][i]))
    im.save(path)


def decryptImage(path, p0c0):
    im = Image.open(in_img)
    size = im.size
    pic = np.array(im)
    im.close()
    r1 = Decimal('0.478706063089473894123')
    r2 = Decimal('0.613494245341234672318')
    r3 = Decimal('0.946365754637812381837')
    w, h = size
    const = 10 ** 14
    for _ in range(200):
        r1 = f1(r1)
        r2 = f2(r2)
        r3 = f3(r3)
    r1_list, r2_list = [], []
    for _ in range(w * h):
        r1_list.append(r1)
        r2_list.append(r2)
        r1 = f1(r1)
        r2 = f2(r2)
    p0 = p0c0[0]
    c0 = p0c0[1]
    for x in range(w):
        for y in range(h):
            k = int(round(const * r3)) % 256
            k = bin(k)[2:].ljust(8, '0')
            k = int(k[p0 % 8:] + k[:p0 % 8], 2)
            r3 = f3(r3)
            pic[y, x] = ((pic[y, x] ^ c0 ^ k) - k) % 256
            c0 = k ^ ((k + pic[y, x]) % 256) ^ c0
            p0 = pic[y, x]
    for x in range(w-1, -1, -1):
        for y in range(h-1, -1, -1):
            x1 = int(round(const*r1_list.pop())) % w
            y1 = int(round(const*r2_list.pop())) % h
            pic[y, x], pic[y1, x1] = pic[y1, x1], pic[y, x]
    outputImage(path, pic, size)


in_img = 'flag_enc.bmp'
i = 1
for p in range(100, 105):
    for c in range(200, 205):
        decryptImage(str(i)+'.bmp', (p, c))
        i += 1

UIUCTF 2021

Re-hvhpgs{synt}

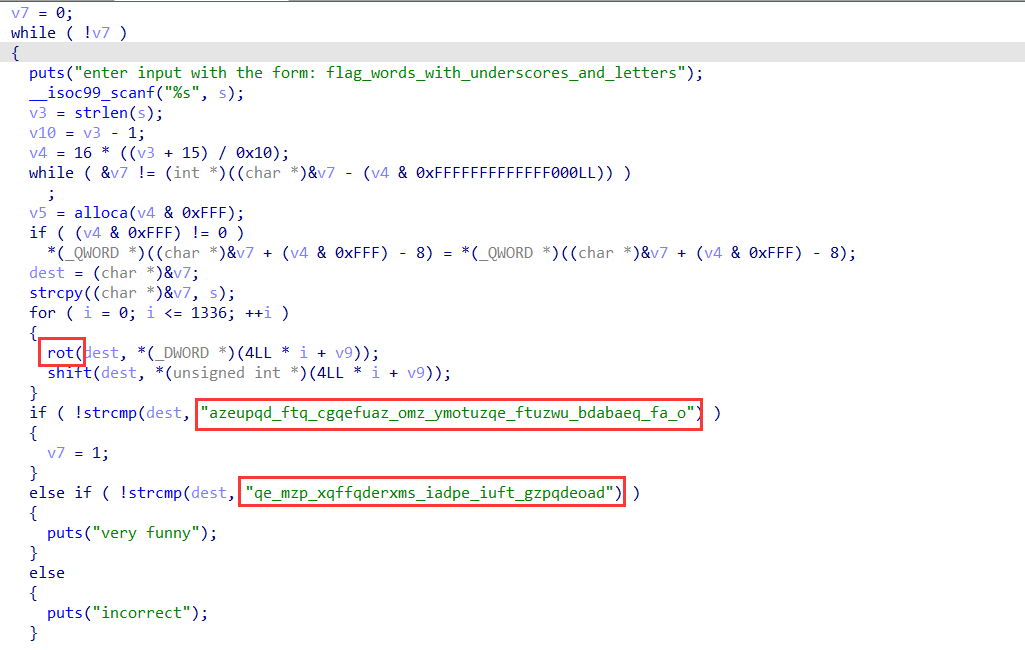
image-20210731121038121

首先看到最显眼的两串字符，词频一下可以出来有含义的字符，然后发现是rot和位移，直接手撕了，输入i_propose_to_consider_the_question_can_machines_think就可以得到flag

Crypto-dhke_intro

题目提示

Small numbers are bad in cryptography. This is why.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
import random
from Crypto.Cipher import AES

# generate key
gpList = [ [13, 19], [7, 17], [3, 31], [13, 19], [17, 23], [2, 29] ]
g, p = random.choice(gpList)
a = random.randint(1, p)
b = random.randint(1, p)
k = pow(g, a * b, p)
k = str(k)

# print("Diffie-Hellman key exchange outputs")
# print("Public key: ", g, p)
# print("Jotaro sends: ", aNum)
# print("Dio sends: ", bNum)
# print()

# pad key to 16 bytes (128bit)
key = ""
i = 0
padding = "uiuctf2021uiuctf2021"
while (16 - len(key) != len(k)):
    key = key + padding[i]
    i += 1
key = key + k
key = bytes(key, encoding='ascii')

with open('flag.txt', 'rb') as f:
    flag = f.read()

iv = bytes("kono DIO daaaaaa", encoding = 'ascii')
cipher = AES.new(key, AES.MODE_CFB, iv)
ciphertext = cipher.encrypt(flag)

print(ciphertext.hex())

看提示是要Diffie–Hellman密钥交换，但都可以爆破，注意下hex编码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
# !/usr/bin/env python
# -*- coding:utf-8 -*-
from Crypto.Cipher import AES
from binascii import unhexlify

ciphertext = 'b31699d587f7daf8f6b23b30cfee0edca5d6a3594cd53e1646b9e72de6fc44fe7ad40f0ea6'
gpList = [[13, 19], [7, 17], [3, 31], [13, 19], [17, 23], [2, 29]]
iv = bytes("kono DIO daaaaaa", encoding='ascii')
for g, p in gpList:
	for a in range(1, p+1):
		for b in range(1, p+1):
			k = str(pow(g, a * b, p))
			key = ''
			i = 0
			padding = 'uiuctf2021uiuctf2021'
			while 16 - len(key) != len(k):
				key = key + padding[i]
				i += 1
			key = key + k
			key = bytes(key, encoding='ascii')
			cipher = AES.new(key, AES.MODE_CFB, iv)
			flag = cipher.decrypt(unhexlify(ciphertext))
			if flag.startswith(b'uiuctf'):
				print(flag)

Crypto-back_to_basics

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
from Crypto.Util.number import long_to_bytes, bytes_to_long
from gmpy2 import mpz, to_binary
#from secret import flag, key

ALPHABET = bytearray(b"0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZ#")

def base_n_encode(bytes_in, base):
	return mpz(bytes_to_long(bytes_in)).digits(base).upper().encode()

def base_n_decode(bytes_in, base):
	bytes_out = to_binary(mpz(bytes_in, base=base))[:1:-1]
	return bytes_out

def encrypt(bytes_in, key):
	out = bytes_in
	for i in key:
		print(i)
		out = base_n_encode(out, ALPHABET.index(i))
	return out

def decrypt(bytes_in, key):
	out = bytes_in
	for i in key:
		out = base_n_decode(out, ALPHABET.index(i))
	return out

"""
flag_enc = encrypt(flag, key)
f = open("flag_enc", "wb")
f.write(flag_enc)
f.close()
"""

当然还有一个flag_enc文件

挺有意思的题目，就是2~36进制的转换，关键函数

1
2
3
def base_n_decode(bytes_in, base):
	bytes_out = long_to_bytes(int(bytes_in, base=base))
	return bytes_out

Python的int真好用

手撕的，因为有些比如key的最后一位是W进制，但是U和V也没在密文里出现

Crypto-dhke_adventure

又是jo厨师傅出的题，很明显的离散对数系统的密码题，因为hint有smoother，可以想到是解离散对数的光滑数问题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
from random import randint
from Crypto.Util.number import isPrime
from Crypto.Cipher import AES
from hashlib import sha256

print("I'm too lazy to find parameters for my DHKE, choose for me.")
print("Enter prime at least 1024 at most 2048 bits: ")
# get user's choice of p
p = input()
p = int(p)
# check prime valid
if p.bit_length() < 1024 or p.bit_length() > 2048 or not isPrime(p):
    exit("Invalid input.")
# prepare for key exchange
g = 2
a = randint(2,p-1)
b = randint(2,p-1)
# generate key
dio = pow(g,a,p)
jotaro = pow(g,b,p)
key = pow(dio,b,p)
key = sha256(str(key).encode()).digest()

with open('flag.txt', 'rb') as f:
    flag = f.read()

iv = b'uiuctf2021uiuctf'
cipher = AES.new(key, AES.MODE_CFB, iv)
ciphertext = cipher.encrypt(flag)

print("Dio sends: ", dio)
print("Jotaro sends: ", jotaro)
print("Ciphertext: ", ciphertext.hex())

已知

$dio=g^a\ mod\ p$

$jotaro=g^b\ mod\ p$

$key=dio^b\ mod\ p$

解题的关键是p可以由攻击者提供的，那直接提供一个光滑数+1好了，这样这个DLP离散对数求解的难题就变得可计算了，具体的推导参考pohlig-hellman攻击原理，有能力可以复现

这里直接上脚本了，首先生成一个光滑数

1
2
3
4
5
6
7
8
9
10
11
from Crypto.Util.number import *
from gmpy2 import *

item = 2
p = 1
while 1:
    p *= item
    item = next_prime(item)
    if 1024 < p.bit_length() < 2048 and isPrime(p + 1):
        print(p+1)
        break

直接手动接收，然后在sgae里求a和b

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
#!/usr/bin/env python
# -*- coding: utf-8 -*-
from Crypto.Cipher import AES
from binascii import unhexlify
from hashlib import sha256

p = 20404068993016374194542464172774607695659797117423121913227131032339026169175929902244453757410468728842929862271605567818821685490676661985389839958622802465986881376139404138376153096103140834665563646740160279755212317501356863003638612390661668406235422311783742390510526587257026500302696834793248526734305801634165948702506367176701233298064616663553716975429048751575597150417381063934255689124486029492908966644747931
a = 1706514538409217609380184471483970486111601581179909732547081795755601848099714892783660477820125268651686071436129197042742970850298506167342840465201954449860957095450958345421698689291401652404764413822088773220645950460091121901749681603487210460064157239812734204314334694247020508700704643391774792654182943517813353983667531492481271292815208332729128642069655591289999915464139472699283049217926350224615448461688066
b = 14466632275269913037069509287532932279884213206515600538938395240468925268146374104530207395909468350257778074856758057525057561502009116834555962090895520108072724285442706303410135968614985268443945781896987070215220814783356743958044861941110284092061774699164461968593879814604175818707171934938878476262296832165434644133455246857171139473183371584687955863862012348287764247314297996868855594079156695942227229848338865
dio = 16167922424137241666246302388507094614219683075656937696624976269971219170930381539629329712953190516880647147637220034502113432117052541565403357952291692484827614380683288824529855182911429985823152492290185107775580207164746921109360997835543504066225649925051809637197356760554700827177215351020335554912004088973554778245562345835228507025035376705826984822212122075068467338353809039042992813485576139824709322511611135
assert dio == pow(g, a, p)
assert jotaro == pow(g, b, p)
key = pow(dio, b, p)
key = sha256(str(key).encode()).digest()
jo = 8478318935358501390014596426908185869306605857407596116840606911586830527583698320042764633027826654399751539088096707226001027141331485792640154020208368663060333097725346477808040686885134694513306486060638308544451042554707764114958622916238232491752753035945375341164707378481832386716731243612254449779955395389475168461403985894687650228947467124029857674022920610930987210652487673276585269753595356252512713370074208
ciphertext = 'f21c554f4e520e3122eb9708bd88de356b7d0d8d9728536b39d22b706afcdaecd7bed753666a763f8c0d'
iv = b'uiuctf2021uiuctf'
cipher = AES.new(key, AES.MODE_CFB, iv)
flag = cipher.decrypt(unhexlify(ciphertext))
print(flag)

Crypto CTF

Farm

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
#!/usr/bin/env sage

from sage.all import *
import string, base64, math
from flag import flag

ALPHABET = string.printable[:62] + '\\='

F = list(GF(64))

def keygen(l):
	key = [F[randint(1, 63)] for _ in range(l)] 
	key = math.prod(key) # Optimization the key length :D
	return key

def maptofarm(c):
	assert c in ALPHABET
	return F[ALPHABET.index(c)]

def encrypt(msg, key):
	m64 = base64.b64encode(msg)
	enc, pkey = '', key**5 + key**3 + key**2 + 1
	for m in m64:
		enc += ALPHABET[F.index(pkey * maptofarm(chr(m)))]
	return enc

# KEEP IT SECRET 
key = keygen(14) # I think 64**14 > 2**64 is not brute-forcible :P

enc = encrypt(flag, key)
print(f'enc = {enc}')

image-20210812224123276

就是类似字典key和value的关系，关键的key爆破下就好了。贴下脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
import string
import base64
enc = '805c9GMYuD5RefTmabUNfS9N9YrkwbAbdZE0df91uCEytcoy9FDSbZ8Ay8jj'
ALPHABET = string.printable[:62] + '\\='

F = list(GF(64))

for pkey in F:
    c = ''
    for i in enc:
        p1 = ALPHABET.index(i)
        p2 = 0
        if pkey!= 0:
            p2 = F.index(F[p1] / pkey)
        c += ALPHABET[p2]
    try:
        print(base64.b64decode(c))
    except:
        pass

然后在64个结果中找flag

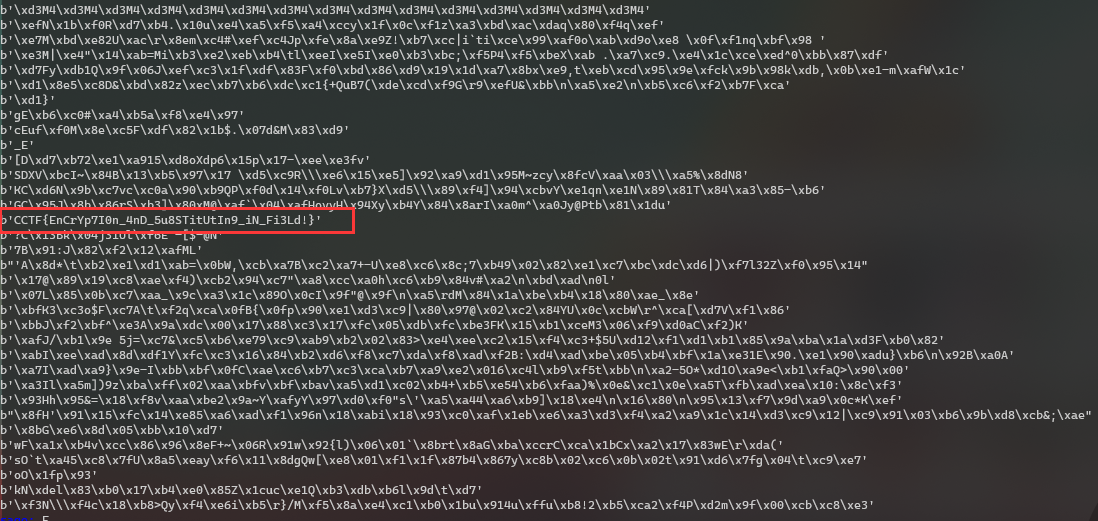
image-20210812224334985

1
CCTF{EnCrYp7I0n_4nD_5u8STitUtIn9_iN_Fi3Ld!}